Evolution and crystallization of Lie algebras
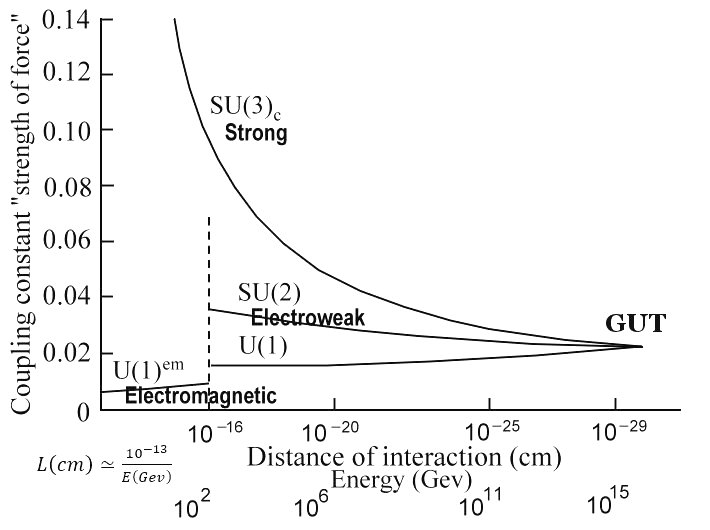
The Grand Unified Theory (GUT) proposes that the Standard Model gauge groups SU(3) × SU(2) × U(1) can be combined into a single gauge group, commonly theorized to be SU(5), SU(10), or E6. The unified group is believed to have been spontaneously broken into the Standard Model subgroup below a very high energy scale.
The standard model is a quantum field theory in which particles are excited states of the fermion fields, ψ, which account for matter particles, the electroweak boson fields W1, W2, W3, gluon field Ga, and the Higgs field φ. The standard model QFT uses a gauge theory formulation to describe physical behavior of discrete particles via a Lagrangian that is invariant to local transformations of a continuous field. The transformations between possible gauges, called gauge transformations, form a Lie group which is a continuous group described by a Lie algebra of group generators. If the symmetry group is non-commutative, then the gauge theory is referred to as non-abelian and can be described with Yang–Mills theory. Yang–Mills theory describes the behavior of elementary particles using non-abelian Lie groups and are at the core of the unification of the electromagnetic force and weak forces (i.e. U(1) × SU(2)) as well as quantum chromodynamics which is the theory of the strong nuclear force (i.e. SU(3)).
Gauge connections are covariant derivatives and can be structured into a reduced continuous moduli space (a gauge field). The gauge field strength is the curvature of the connection, and the energy of the gauge field is given by the Yang–Mills action functional. Applying the Euler–Lagrange equations to this functional gives rise to its critical points. These critical points are connections that are either the absolute or local minima of the functional and minimize their curvature resulting in natural descriptions of the motion of particles in the field via the principle of least action.
This diagram depicts interactions of elementary particles: the top row of vertices (leptons and quarks) are the matter particles; the second row of vertices (photon, W/Z bosons, gluons) are the force mediating particles; and the bottom row is the Higgs boson.
The Higgs field is a scalar field with two neutral and two electrically charged components. Its "Mexican hat-shaped" potential leads it to take a nonzero value everywhere which breaks the weak isospin symmetry of the electroweak interaction and, via Yukawa coupling, gives mass to massless quark and lepton fields (i.e., the fundamental fermion particles). Through spontaneous symmetry breaking, these fermions acquire a mass proportional to the vacuum expectation value of the Higgs field. This effect occurs because scalar field components of the Higgs field are "absorbed" by the massive bosons as degrees of freedom and couple to the fermions (via Yukawa coupling) thereby producing the expected mass terms. Roughly speaking, we can think of the Higgs field as being an asymmetric field that is the resonant inverse of the lepton field which cancels out energy to match the vacuum expectation resulting in a mass term. W+/- and Z bosons do not have Yukawa coupling, and instead derive their mass from the weak charge of the Higgs field itself.
A lepton is an elementary particle of half-integer spin (spin 1⁄2) that does not undergo strong interactions. Two main classes of leptons exist: charged leptons (also known as the electron-like leptons or muons), and neutral leptons (better known as neutrinos). Charged leptons can combine with other particles to form various composite particles such as atoms and positronium, while neutrinos rarely interact with anything, and are consequently rarely observed. The best known of all leptons is the electron.
“Protons” are now known to be composite particles, containing three valence quarks, and together with neutrons are now classified as hadrons. Protons are composed of two up quarks of charge +2/3e and one down quark of charge −1/3e. The rest masses of quarks contribute only about 1% of a proton's mass. The remainder of a proton's mass is due to quantum chromodynamics binding energy, which includes the kinetic energy of the quarks and the energy of the gluon fields that bind the quarks together.
Despite being a collage of mathematical patchwork, the Standard Model is the most well validated and successful theory of particle physics. Measurements of electron magnetic moment of electrons agree with the standard model’s prediction to 0.13 parts per trillion, or roughly 0.1 billionths of a percent (0.000000000013%), which is the most precise measurement of any property of an elementary particle.
An electron can be described by its quantum numbers.
The irreducible representations (irreps) of the SO(3) Lie group of rotations relates to the orbital shape and angular momentum of quantum number ℓ. Values of ℓ = 0, 1, 2, 3 correspond to the s, p, d orbitals. The shape of these orbitals can be expressed with parameterized spherical harmonic equations. Counting the 4s, 4p, 4d and 4f orbitals makes a total of 16 orbitals in the fourth and highest energy level.
Left: hydrogen p-orbital with varying values of m=+1 to -1. Right: hydrogen 3p-orbital with varying values of m=+1 to -1
Sampled electron density varies to be lowest near the nucleus with peaks forming subshells. There is a surface between the two subshells where there is zero probability of finding an electron, known as a node or a nodal surface.
In an ordinary nucleus composed of protons and neutrons, The atomic number is the number of protons (non-electron leptons) found in the nucleus of every atom of that element. The atomic number alone determines the chemical properties of an element; thus an element can be defined as consisting of any mixture of atoms with a given atomic number. Electronegativity decreases as we move down a given group and increases as we move from left to right across a period.
Quantum numbers specify the shape of an atomic orbital and the number of valence electrons (i.e. the number of electrons in the outermost shell) which influences possible chemical bonds and bond angles. Covalent bonds are formed between atoms when they share electrons. Fermions are ionic bonds formed when ions with positive charges (cations) are in close proximity to ions with negative charges (anions). Metallic bonding involves sharing of free electrons among a structure of positively charged ions (cations).
The number of electrons in each element's electron shells, particularly the outermost valence shell, is the primary factor in determining its chemical bonding behavior.
(Carbon-60, C60, or fullerene is a rare, spherically-structured molecule composed of 60 carbon atoms)
Aside from covalent bonds, interatomic/intramolecular interactions involve more subtle interactions within molecules.
Electron spin also plays a subtle role in intermolecular interactions. Spin s = ½ or -½, determines if an atom produces magnetism. The spin generates an electric current and causes each electron to act like a microscopic magnet. In most substances, equal numbers of electrons spin in opposite directions, which cancels out their magnetism.
Hydrogen bonding occurs in molecules that have a hydrogen atom covalently bonded to an atom that is electronegative. Keesom forces are the forces between the permanent dipoles of two polar molecules. Van der Waals forces result from a transient shift in electron density to one side of the nucleus that generates a transient charge which a nearby atom can be attracted to or repelled by.
The Lie theory description of charge, magnetism and spin is also of interest. Charge corresponds to the time-invariant generators of their corresponding symmetry group. Intuitively, charge is perceived and thought of as a dynamic force which results from compounding flow through the symmetries of the gauge field. In the case of electromagnetism, electric charge is generated from an abelian field 𝑈(1) gauge field. The notion of time-invariance aligns with the advent of transitioning from Lagrangian to Hamiltonian dynamics, as charge generators are those that commute with the Hamiltonian.
Charges are often denoted by the letter Q, and so the invariance of the charge corresponds to the vanishing commutator [ Q , H ] = 0 [ Q, H ] = 0, where H is the Hamiltonian. Thus, charges are associated with conserved quantum numbers; these are the eigenvalues q of the generator Q. The thing that "flows" in the current is the "charge", the charge is the generator of the (local) symmetry group. This charge is sometimes called the Noether charge.
This animation shows how the electric field transitions into a point-shaped electric dipole, which consists of two point electric charges of opposite polarity located close together.
The reason electromagnetism is abelian or 𝑈(1) is because there is only one electric charge 𝑒, with positive and negative values, while other gauge fields have an array of color-charges. Expanding away from abelien constraints with Yang-mills theory, allows us to categorize other forces.
Like in Yukawa coupling of mass generation, charge is a coupling term that describes interactions of particles with a field in terms of a degree of freedom. In this case charge is a degree of freedom w.r.t to the invariant of time. Instead of focusing only on time-invariants, closely tied to the Hamilton picture of dynamics, we can explore degrees of freedom associated with the Lie group itself.
Divergence in one-to-one correspondence of the representations of a Lie group and its Lie algebra results in fractional 1/2 spin. Recall, the exponential map sends a Lie algebra to its Lie group, capturing local group structure. Fractional spin characterizes the distinction between bosons (force particles) and fermions (matter particles) since only fermions may have half-integer spin. Particles with integer spin occupy symmetric quantum states and have symmetric wave function ψ(A, B) = ψ(B, A), while particles with half-integer spin occupy antisymmetric states and have an antisymmetric wave function, ψ(A, B) = - ψ(B, A).
The Pauli exclusion principle states that two or more identical particles with half-integer spins (i.e. fermions) cannot occupy the same quantum state simultaneously (i.e. possess the same quantum numbers). Roughly speaking, bosons have a tendency to occupy the same quantum state, which underlies phenomena such as the laser, Bose–Einstein condensation, and superfluidity. Fermions, on the other hand, are forbidden from sharing quantum states, giving rise to much of chemistry and material. For example, if two electrons reside in the same orbital, then their n, ℓ, and m values are the same; therefore their m values must be different, and thus the electrons have opposite half-integer spin of 1/2 and −1/2.
Magnetic structure of a material pertains to the ordered arrangement of magnetic spins, typically within an ordered crystallographic lattice. For localized magnetism, many magnetic structures can be described by magnetic space groups, which give a precise accounting for all possible symmetry groups of up/down configurations in a three-dimensional crystal. However, this formalism is unable to account for some more complex magnetic structures, such as those found in helimagnetism. For ferromagnetism in the ground state, there is a common spin quantization axis and a global excess of electrons of a given spin quantum number, there are more electrons pointing in one direction than in the other, giving a macroscopic magnetization. In antiferromagnetism, there is still a common quantization axis, but the electronic spins are pointing alternatingly up and down, leading again to cancellation of the macroscopic magnetization. However, specifically in the case of frustration of the interactions, the resulting structures can become much more complicated, with inherently three-dimensional orientations of the local spins. Finally, ferrimagnetism, as prototypically displayed by magnetite, is in some sense an intermediate case: here the magnetization is globally uncompensated as in ferromagnetism, but the local magnetization points in different directions.
Like ferromagnetism and atomic spectral lines, superconductivity is a phenomenon which can only be explained by quantum mechanics. It is characterized by the Meissner effect, the complete cancellation of the magnetic field in the interior of the superconductor during its transitions into the superconducting state. The Meissner effect, the state of zero resistance, is the quantization of the magnetic flux or permanent currents. The occurrence of the Meissner effect indicates that superconductivity cannot simply be understood as the idealization of perfect conductivity in classical physics. The existence of these "universal" properties is rooted in the nature of the broken symmetry of the superconductor and the emergence of off-diagonal long range order. Off diagonal long range order is closely connected to the formation of Cooper pairs.
Molecular geometry is determined by the central atom and the surrounding atoms and electron pairs. The crystallographic space groups describe these idealized groups of symmetries in 3d-space.
Configurations of valence electrons can also cause bent structures and irregularities in molecules that prevent periodic lattices from compounding and work against the crystallization of molecules. This aspect of subtle intramolecular forces makes the difference between a material made of 2-d planar lattices, a crystal made of 3-d polytopes, or biological matter made of less ordered molecules. A lone pair refers to a pair of valence electrons that are not shared with another atom in a covalent bond.
The shape of most molecules can be predicted using the Valence Shell Electron Pair Repulsion (VSEPR) method. VSEPR makes a distinction between electron group geometry, which expresses how electron groups (bonds and nonbonding electron pairs) are arranged, and molecular geometry, which expresses how the atoms in a molecule are arranged. However, the two geometries are related. There are two types of electron groups: any type of bond—single, double, or triple—and lone electron pairs. Although the electron groups are oriented in the shape of a tetrahedron, from a molecular geometry perspective, the shape of NH3 is trigonal pyramidal. Although the electron groups are oriented in the shape of a tetrahedron, the shape of the molecule is bent or angular
Many reactive nonmetals are important in biological systems. Nonmetals have structures that are very different from those of the metals, primarily because they have greater electronegativity and electrons that are more tightly bound to individual atoms. Metals crystallize in closely packed arrays that do not contain molecules or covalent bonds. Nonmetal structures contain covalent bonds, and many nonmetals consist of individual molecules. The electrons in nonmetals are localized in covalent bonds, whereas in a metal, there is delocalization of the electrons throughout the solid.
The first member of each group of the nonmetals has only four valence orbitals (one 2s and three 2p) available for bonding, whereas other group members have empty d orbitals in their valence shells, making possible five, six, or even more bonds around the central atom. For example, nitrogen forms only NF3, whereas phosphorus forms both PF3 and PF5. The variety of oxidation states displayed by most of the nonmetals means that many of their chemical reactions involve changes in oxidation state through oxidation-reduction reactions. Nonmetals oxidize most metals. With the exception of most of the noble gasses, all nonmetals form compounds with oxygen, yielding covalent oxides. Under normal conditions, more than half of the nonmetals are gasses, one is a liquid, and the rest include some of the softest and hardest of solids. They include the most reactive and least reactive of elements, and they form many different ionic and covalent compounds. The noble gasses are all monatomic, whereas the other nonmetal gasses—hydrogen, nitrogen, oxygen, fluorine, and chlorine—normally exist as the diatomic molecules H2, N2, O2, F2, and Cl2
In addition to crystallographic space groups there are also magnetic space groups. These symmetries treat time as an additional dimension, and the group elements can include time reversal as reflection in it. The time reversal element flips a magnetic spin while leaving all other structures the same and it can be combined with a number of other symmetry elements. Including time reversal there are 1651 magnetic space groups in 3D.
Crystal structure of a molecular trefoil knot with two copper(I) templating ions bound within it
Nucleotides are constructed from sugar molecules (either ribose in RNA or deoxyribose in DNA) attached to a phosphate group and a nitrogen-containing base.
RNA molecules have a backbone made of alternating phosphate groups and the sugar ribose (rather than the deoxyribose found in DNA).
mRNA sequences contain condon subsequences of three nucleotides (ACGTU). There are 64 different codons: 61 specify amino acids and 3 are used as stop signals. Codons bind with matching base pairing of tRNA that carry one of twenty-one amino acids.
A constructed amino acid chain then folds into a protein structure which interacts with other proteins. Both the folding and interactions depend on the electric charges and hydrophobic property of their side chains. These interactions form pathways that contribute to the development of phenotypes.
Note, primary structure is the linear sequence of amino acids, secondary structure is the local spatial conformation of the polypeptide backbone excluding the side chains, tertiary structure is the three dimensional shape of a protein determined by side chains, quaternary structure refers to the structure of proteins which are themselves composed of two or more smaller protein chains
Biological pathways can be generalized into three categories. Metabolic pathways involve chemical reactions that occur in our bodies, gene-regulation pathways turn genes on and off, and signal transduction pathways move a signal from a cell's exterior to its interior.
GPCRs are involved in a wide variety of physiological processes. Some examples of their physiological roles include: The visual sense, the gustatory sense (taste), The sense of smell, Behavioral and mood regulation (receptors for serotonin, dopamine, histamine, GABA, and glutamate), regulation of immune system activity and inflammation, Autonomic nervous system transmission: - Cell density sensing: A novel GPCR role in regulating cell density sensing, Homeostasis modulation (e.g., water balance), involved in growth and metastasis of some types of tumors, Used in the endocrine system for peptide and amino-acid derivative hormones that bind to GCPRs on the cell membrane of a target cell. This activates cAMP, which in turn activates several kinases, allowing for a cellular response, such as transcription.
The 5-HT2C receptor is a G protein-coupled receptor (GPCR) that binds the endogenous neurotransmitter serotonin (5-hydroxytryptamine, 5-HT). 5-HT receptors are the target of a variety of pharmaceutical and recreational drugs, including many antidepressants, antipsychotics, hallucinogens, and more.
X-Ray crystallography has historically been used to accurately reconstruct the atomic positions of a folded protein. It works by embedding a protein into a crystal then mechanically rotating it while shooting it with X-ray (or other diffused) beams of energy and then inferring coordinates and angles of aligned atoms. Diffused streams of electrons from electrically charged beams can be fine-tuned to produce strong enough energy to penetrate varying densities of matter to capture a desired layer.
This process can be interpreted as finding invariants of the connected 3-D embedded points (i.e. a graph) to the SO(3) Lie group action.
Alphafold2 used coordinate data from these X-ray crystallography measurements to train its models to predict protein folds when only given an amino acid sequence. In contrast to predicting folded structures via simulating molecular dynamics, the deep learning model makes inferences of the predicted structure based on crystallography data it had previously been trained on.
To achieve this while having limited examples, a transformer-like graph neural network relied on an attention mechanism known as Invariant Point Attention. IPA has an inductive bias that conforms its latent representations using actions of the Euclidean group E(n), i.e. all translations, rotations, and reflections of Euclidean space. Note, rotation alone is SO(3) while rotation and reflection together comprise O(3).
This inductive bias allows the model to rotate, translate, and reflect atoms so that it learns representations that are invariant to these actions and “places” similar representations of protein structures near each other in its latent space.
In the case of E(3), the model relies on a key insight - that rotating, translating, or reflecting coordinates does not change their distances (isometries). This means the approach of using parameterized spherical harmonics works well for scalar features (i.e. intra-atomic potential energy), but vectors of higher dimensions need to appropriately transform (i.e. interatomic potential energy/force fields).
Using neural networks for learning parametrizations of spherical harmonics is quite different than the previous methods but may still benefit from mathematical insights of previous approaches.Some progress has been made with geometric tensors, which characterize generic equations of all possible transformations and then learn parameters of function via machine learning models, i.e: Multi-Atomic Cluster Expansion (MACE).
Like the orbital quantum number ℓ, E(3)-equivariance uses spherical harmonics, which are basis functions for irreducible representations of SO(3). Wigner D-matrices are pre-defined unitary matrices of irreps of the groups SU(2) and SO(3) that can be parameterized when learning these spherical harmonics. In particular, the Kronecker product of the irrep D-matrix creates irreducible components using Clebsch–Gordan coefficients as parameters.
Given the evolutionary pressures on proteins over time in terms of fitness and function of their phenotypes within dynamic biological pathways, we can speculate that the deep learning model also learns how the proteins structurally evolve through their conserved and mutated motifs over time. In this sense, the model also learns a “time crystal” of the evolution of biologic information as encoded by proteins in 3d space.
Note, isoelectronicity is a phenomenon observed when two or more molecules have the same structure (positions and connectivities among atoms) and the same electronic configurations, but differ by what specific elements are at certain locations in the structure. Identifying a compound as isoelectronic with one already characterized offers clues to possible properties and reactions (Differences in properties such as electronegativity of the atoms in isoelectronic species can affect reactivity.)
This organization of evolutionary relationships is not dissimilar to constructions of phylogenetic trees in the study of phylogeny. We can imagine molecule speciation as pathways flowing through a latent space connecting variations of latent representations. In an energy-based model framework, we can think of genetic material as navigating this high-dimensional energy landscape in order to survive via niche construction and replication. Since phenotypes are mediated by biological pathways which are in turn mediated by interactions of proteins, we can infer there is a structural essence underlying phenotypes.
It’s also worth noting the efficacy and generalizability of Transformers in large language models. In LLMs there is no inductive bias and instead the model is trained on a massive dataset and learns/memorizes reducible but flexible representations instead of irreducible ones. It can also be speculated that these models develop a latent space that evolves in time as well. Thus it too is comparable to a time crystal with the evolution of symbolic information encoded as text in 2d space (sequences). Here the model learns stable memetic structures over the time of written/typed language.
https://math.stackexchange.com/a/764753
A coxeter diagram is a way of describing a group generated by reflections. Any collection of reflections (in Euclidean space, say) will generate a group. To know what this group is like, you need to know more than just how many generators there are: you need to know the relationships between the generators. The Coxeter diagram tells you that information. There is a node for each generator, and an edge between the two labeled with the order of their product.
Given a Coxeter diagram with 𝑛 nodes, you can construct reflections in 𝑛-dimensional space to realize the Coxeter group. We'll identify reflection isometries with their hyperplane of reflection. To get the product of reflections to have order 𝑝, you want their hyperplanes of reflection at an angle of 𝜋/𝑝 to each other, since the composition of the two reflections is a rotation by twice the angle between them. The composition would have the same order with an angle of 𝑚𝜋/𝑝, where 𝑚 is relatively prime to 𝑝. The group generated ends up being the same, so you might as well work with the hyperplanes at an angle of 𝜋/𝑝.
So with , 𝜌0 and 𝜌1 should form an angle of 𝜋/4 (or 45°), 𝜌0 and 𝜌2 should form an angle of 𝜋/2 (or 90°), and 𝜌1 and 𝜌2 should form an angle of 𝜋/3 (or 60°).
For example, Start with two planes which are orthogonal to eachother: call them 𝜌0 and 𝜌2.. Stick in a plane which forms an angle of 45° with 𝜌0; you can start with it also being orthogonal to 𝜌2, so we have the situation in depicted in this picture. On the left, we have transparent plane segments; on the right, they are opaque. Think of 𝜌2 as the horizontal plane, 𝜌0 as the vertical plane coming straight out of the page, and the "new plane" (intended to be 𝜌1) as the plane going from corner to corner.
Then rotate the new plane, keeping it at 45° with 𝜌0, until it forms an angle of 60° with 𝜌2. You end up with this:
To find a polytope which the group generated by these reflections act on, just pick any point in space and take all its images under the reflections. The convex hull of these points is a polytope acted on by the group. This is known as Wythoff's construction, or a kaleidoscope (because the original point is replicated by all the reflection planes just as a colored dot is replicated in a kaleidoscope). We see that the convex hull of these points is the cube. Many choices of points yield combinatorially identical (or isomorphic) polytopes.
The crystallographic restriction theorem is based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold. Dynkin diagrams differ from Coxeter diagrams, in that they must satisfy crystallographic restriction: only allowing branch labels of 2, 3, 4, and 6 corresponding to rotation angles. Dynkin diagrams correspond to semisimple Lie algebras and are used to classify their root systems.
Using datasets from nature, it seems possible to “crystallize” irreps of various Lie groups into a reduced object. The goal of doing so would be to create a universal graph kernel that may perform generalized representation learning by parameterizing its latent space as a union of manifolds. This idea is developed further using ADE quiver gauge theory. https://lukepereira.github.io/notebooks/documents/2022-gauge-quiver-cnn/main.pdf